Observation of kirchhoff's current law

 Kirchhoff's law

Kirchhoff  law

                                     

Kirchhoff's current law is also known as Kirchhoff's point law of Kirchhoff's junction law. It states that the total algebraic sum of a current flowing to / away from a junction is equal to zero. That is, the total incoming current at any point in the circuit is equal to the total outgoing current.

With this help, we can detect current in one branch of the circuit if other branch currents are known. For example, if a point has three branches and the current coming from branch 1 is 4 amperes. And section 1 emanating from branch 2 is ampere. So Section 4-1 = 3-ampere from branch 3 is outgoing.

Kirchhoff's voltage law or trap law. It states that the algebraic sum of all voltage increases or declines in any closed trap (circuit) is equal to zero.

Voltage increase: -

In a circuit, if we go through the cell in the negative direction it is the voltage increase and from positive to negative it is the voltage drop.

Close circuit or mesh: -

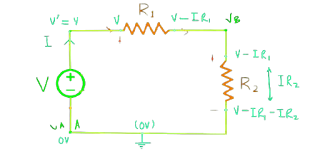
In any complex circuit, we can divide it into several closed loops. A closed-loop circuit is any path in which we start at a point and return to the same point. Using both of these laws, the current flowing across all branches of the network can be calculated. A circuit diagram is given below. In the circuit diagram shown above, we can apply Kirchhoff's current law to any point. KCL at point B. According to it, there are three streams i.e. I, I1, and I2 I = I1 + I2 --------- (1) Similarly, point E. On I = I1 + I2 --------- (2) n The diagram has three loops (mesh or closed circuit) First loop ABCDEFA in cyan color for which the voltage equation is V = I1R1 + I1R2 + I1R3 ------------- (3)

Second loop BGHKEDCB

There is no voltage source in this loop. We start at point B and complete the loop in a clockwise direction. When we move in the direction of the current, the voltage drops and we give it a negative sign. When we move in the opposite direction to the current, the voltage increases and we give it a positive signal. Resistance R4 and R5 have a voltage drop. The resistance R1 R2 and R3 have a voltage increase so the equation is V4 + V5 - V3 -V2 - V1 = 0 ------ (4) I2R4 + I2 R5 - I1R3 - I1R2 - I1R1 ----- (5)

Third loop ABGHKEFA

V - V 4 - V 5 = 0 ----- (6) V = V4 + V5 -------- (7) V = I2R4 + I2 R5 ------ (8) The values ​​of I1 and I2 can be found from the above equations. The above is a simple circuit but any circuit can be solved.